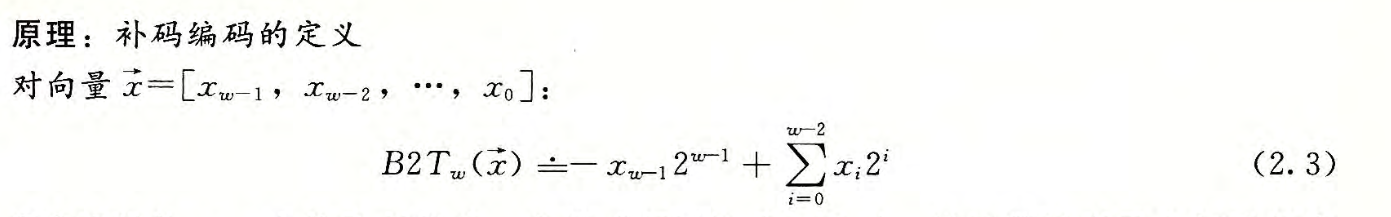信息存储
大部分计算机使用8位的块(或者字节)来作为最小的可寻址的存储器单元。机器级程序将存储器视为一个非常大的字节数组,称之为虚拟存储器。存储器中的每一个字节由唯一的一个地址(address)来标识,所有可能地址的集合称之为虚拟地址空间(virtual address space)
字数据大小
每台计算机都有一个字长 (word size), 指明指针数据的标称大小 (nominal size) 因为虚拟地址是以这样的一个字来编码的,所以字长决定的最重要的系统参数就是虚拟地址空间的最大大小。也就是说,对于一个字长为w位的机器而言,虚拟地址的范围为 O~2^w-1,程序最多访问2^w个字节。
寻址和字节顺序
跨越多字节的程序对象,我们必须建立两个规则:这个对象的地址是什么,以及在内存中如何排列这些字节。在几乎所有的机器上,多字节对象都被存储为连续的字节序列,对象的地址为所使用字节中最小的地址。例如,假设 个类型为 int 的变量 的地址OxlOO, 也就是说,地址表达式 &x 的值为 OxlOO 。那么,(假设数据类型 让为 32 位表示) 节将被存储在内存的 Ox1OO Ox1O1 Ox102 Ox103 位置。
排列表示一个对象的字节方法:
小端法:从低有效字节到高有效字节的顺序存储对象
大端法:从高有效字节到低有效字节的顺序存储对象
C中的移位运算
向左移位运算:右端补0
向右移位运算包含两种形式:逻辑移位(左端补0)和算数移位(左端补最高有效位)
整数表示
无符号数编码
补码编码
有符合数和无符号数的转换
保持位的值不变,改变解释位的方式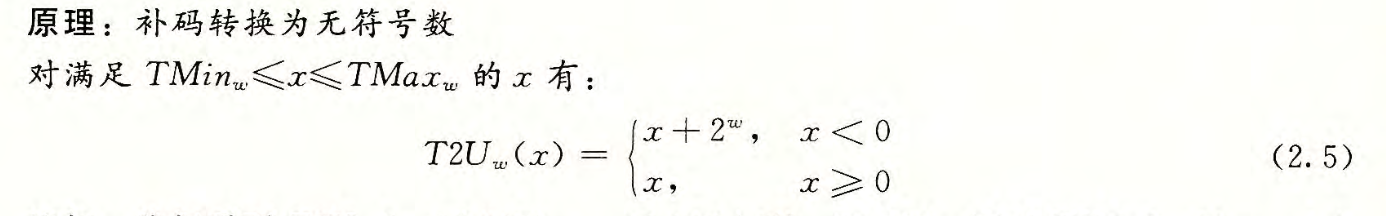
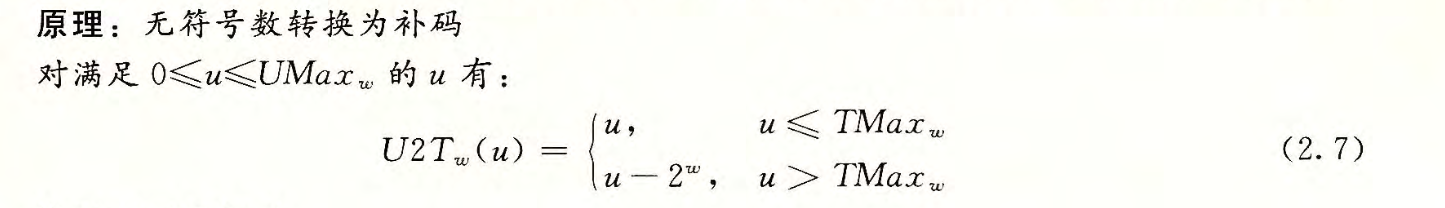
扩展一个数字的位表示
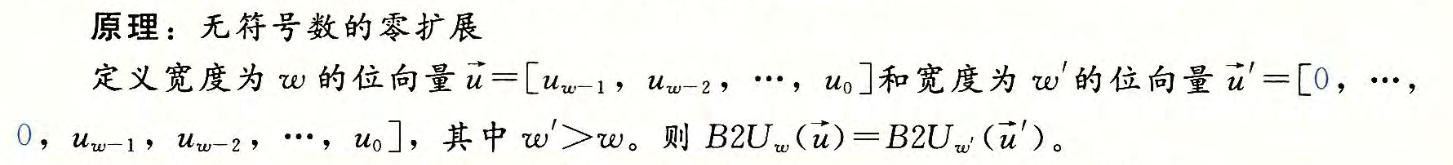
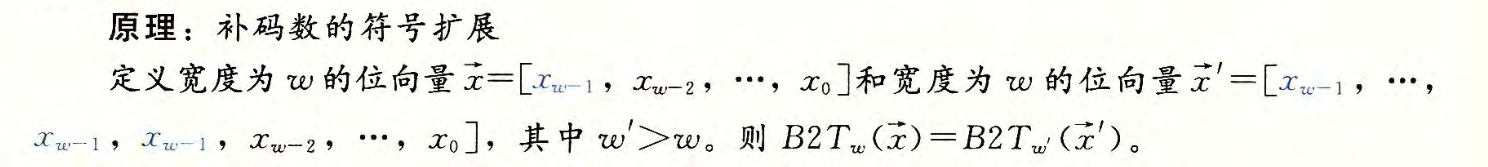
截断数字
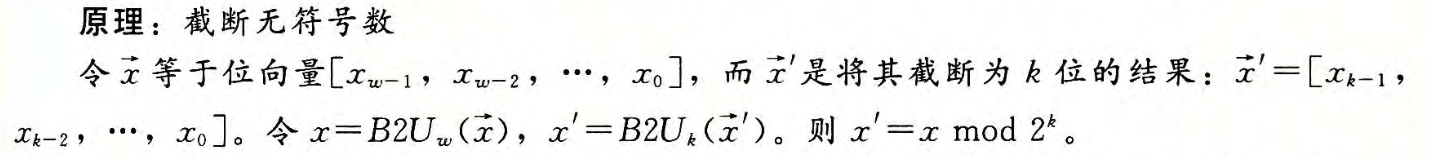
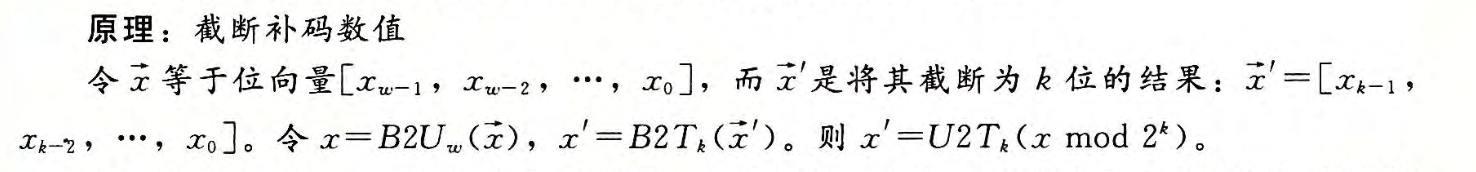
整数运算
乘法
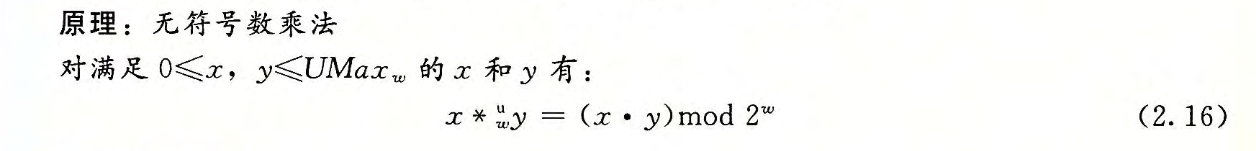
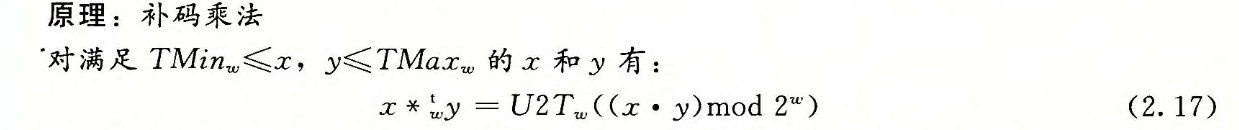
乘以2的幂
在大多数机器上,整数乘法指令相当慢,需要 10 个或者更多的时钟周期,然而其他整数运算(例如加法、减法、位级运算和移位)只需要 1 个时钟周期。因此,编译器使用了一项重要的优化,试着用移位和加法运算的组合来代替乘以常数因子的乘法。

除以2的幂
在大多数机器上,整数除法要比整数乘法更慢——需要 30 个或者更多的周期。除以 2 的幂也可以用移位运算右移来实现,无符号和补码数分别使用逻辑移位和算术移位来达到目的。
浮点数
IEEE浮点表示
用 V = (-1)^sM2^E 的形式来表示一个数:
符号(sign) s决定这个数是负数(s=1)还是正数(s=0),对于数值 0 的符号位解释作为特殊情况处理。
尾数(significand) M 是一个二进制小数,它的范围是 1 ~ 2 - ε,或者是 0 ~ 1 - ε。
阶码(exponent) E 的作用是对浮点数加权,这个权重是 2 的 E 次幂(可能是负数)
将浮点数的位表示划分为三个字段,分别对这些值进行编码:
一个单独的符号位 s 直接编码符号 s。
k 位的阶码字段 exp = e(k-1)…e(1)e(0) 编码阶码 E。
n 位小数字段 frac = f(n-1)…f(1)f(0) 编码尾数 M,但是编码出来的值也依赖于阶码字段的值是否等于 0。
被编码的值的不同情况
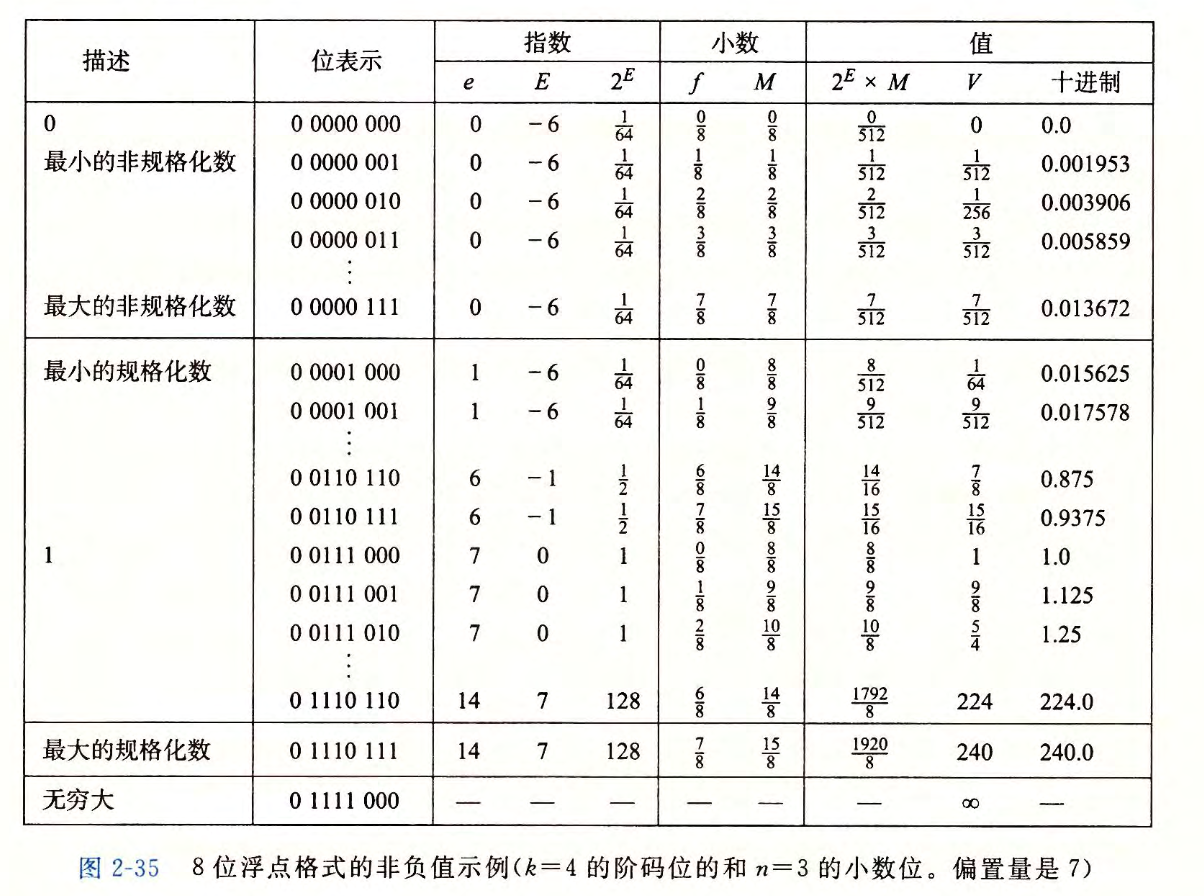
规格化


非规格化
当阶码域为全 0 时,所表示的数是非规格化形式。在这种情况下,阶码值是 E=1-Bias, 而尾数的值是 M=f, 也就是小数字段的值,不包含隐含的开头的 1 。
舍入
因为表示方法限制类浮点数的范围和精度,浮点运算只能近似地表示实数运算。因此,对于值 x,我们一般采用一种系统的方法,能够找到“最接近的”匹配值,这就是舍入运算的任务。
常见的舍入方式有:向偶数舍入、向零舍入、向下舍入、向上舍入
向偶数舍入方式采用的方法是:当舍入位后的数是位于中间值时,它将数字向上或者向下舍入,使得结果的最低有效数字是偶数。因此,这种方法将1.5美元和2.5美元都舍入成2美元。
向偶数舍入法能够运用在二进制小数上。我们将最低有效位的值0认为是偶数,值1认为是奇数。一般来说,只有对形如XX…X.YY…Y1OO…的二进制位模式的数,这种舍入方式才有效,其中X和Y表示任意位值,最右边的Y是要被舍入的位置。